Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 10671 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 37203 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 27-Σεπ-2023 | Ύλη: | 6.3. Η Συνάρτηση ƒ(x) = αx + β | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 37203 | ||
| Ύλη: | 6.3. Η Συνάρτηση ƒ(x) = αx + β | ||
| Τελευταία Ενημέρωση: 27-Σεπ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
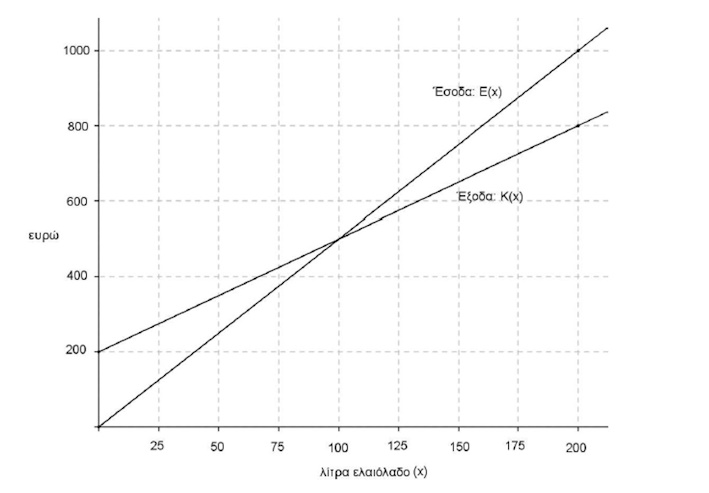
Μια μικρή εταιρεία πουλάει βιολογικό ελαιόλαδο στο διαδίκτυο. Στο παραπάνω σχήμα παρουσιάζεται η γραφική παράσταση της συνάρτησης που περιγράφει τα έξοδα \(K(x)\) και τα έσοδα \(E(x)\) από την πώληση \(x\) λίτρων λαδιού σε ένα μήνα.
α) Να εκτιμήσετε τις συντεταγμένες του σημείου τομής των δύο ευθειών και να ερμηνεύσετε τη σημασία του.
(Μονάδες 6)
β) Ποια είναι τα αρχικά (πάγια) έξοδα της εταιρείας;
(Μονάδες 5)
γ) Πόσα λίτρα ελαιόλαδο πρέπει να πουλήσει η εταιρεία για να μην έχει ζημιά;
(Μονάδες 6)
δ) Να βρείτε τον τύπο των συναρτήσεων \(K(x)\) και \(E(x)\) και να επαληθεύσετε αλγεβρικά την απάντηση του ερωτήματος γ)
(Μονάδες 8)
ΛΥΣΗ
α) Από το γράφημα συμπεραίνουμε ότι το κοινό σημείο των δύο ευθειών είναι κατ’ εκτίμηση το \(Α(100, 500)\).
Η ερμηνεία του είναι η εξής:
Αν η εταιρεία πουλήσει \(100\) λίτρα λάδι, τα έσοδα και τα έξοδα είναι \(500\) ευρώ, δηλαδή δεν έχει ούτε κέρδος ούτε ζημιά.
β) Τα πάγια έξοδα της εταιρείας είναι \(200\) ευρώ, διότι \(K(0)=200\). Δηλαδή ακόμα και αν δεν παραχθεί λάδι \((x=0)\), υπάρχουν έξοδα.
γ) Για να μην έχει η εταιρεία ζημιά πρέπει τα έσοδα να είναι ίσα με τα έξοδα ή μεγαλύτερα από αυτά. Από το γράφημα συμπεραίνουμε ότι αυτό συμβαίνει για παραγωγή \(x\ge 100\) λίτρων λαδιού.
δ) Έστω \(y=ax\) η ζητούμενη εξίσωση της ευθείας \((ε)\) που περιγράφει η συνάρτηση εσόδων \(E(x)\) Η ευθεία αυτή διέρχεται από το σημείο \(Α(100,500)\), οπότε:
$$1000=200α $$ $$\Leftrightarrow α=5$$
Τελικά η ευθεία \((ε)\) έχει εξίσωση;
$$y=5x$$
Επομένως η συνάρτηση των εσόδων είναι \(E(x)=5x\), \(x\ge 0\).
Έστω \(y=α_{1}x+β_{1}\) η ζητούμενη εξίσωση της ευθείας \((ε_{1})\) που περιγράφει η συνάρτηση εξόδων \(Κ(x)\). Η ευθεία \((ε_{1})\) διέρχεται από τα σημεία \(Β(0,200)\) και \(Γ(200,800)\), οπότε έχει συντελεστή διεύθυνσης τον:
$$α_{1}=\dfrac{800-200}{200-0}=\dfrac{600}{200}=3$$
Τότε η ευθεία \((ε_{1})\) γράφεται:
$$y=3x+β_{1}$$
Επειδή η ευθεία \((ε_{1})\) διέρχεται από το σημείο \(Β(0,200)\), οι συντεταγμένες του επαληθεύουν την εξίσωση της. Οπότε:
$$200=0+β_{1} $$ $$\Leftrightarrow β_{1}=200$$
Τελικά η εξίσωση \((ε_{1})\) έχει εξίσωση \(y=3x+200\) και η συνάρτηση των εξόδων είναι:
$$K(x)=3x+200,\ \ x\ge 0$$
Για να μην έχει ζημιά η εταιρεία πρέπει:
$$E(x)\ge K(x) $$ $$\Leftrightarrow 5x\ge 3x+200 $$ $$\Leftrightarrow 2x\ge 200 $$ $$\Leftrightarrow x\ge 100$$
Επομένως η εκτίμηση που κάναμε στο ερώτημα γ) ήταν σωστή.
